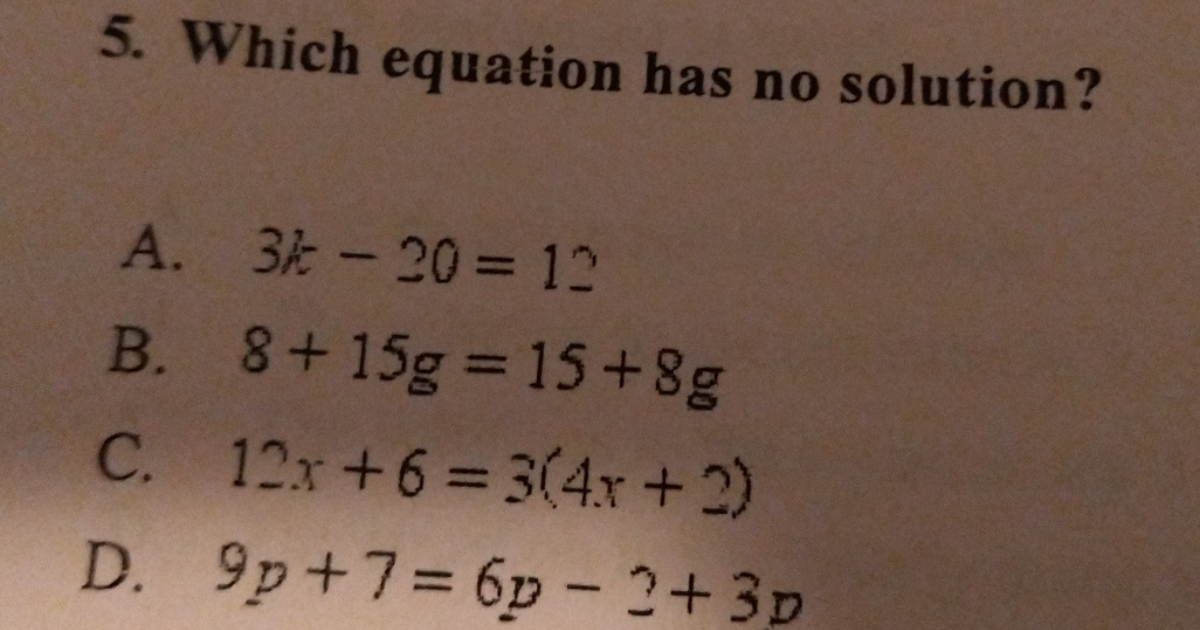In the realm of mathematics, equations are foundational concepts that express the equality of two expressions. Most equations can be solved, meaning we can find values for the variables involved that satisfy the equation. However, some equations, when examined, reveal that no such values exist. This article delves into the concept of equations that have no solutions, providing examples, explanations, and the significance of these equations in various mathematical contexts.
Understanding Equations
An equation is a statement that asserts the equality of two mathematical expressions, typically containing one or more variables. The goal of solving an equation is to determine the values of these variables that make the equation true. Most equations fall into one of three categories:
- Consistent and Independent Equations: These equations have a unique solution.
- Consistent but Dependent Equations: These equations have infinitely many solutions.
- Inconsistent Equations: These are equations that have no solutions.
What is an Equation with No Solution?
An equation with no solution, also known as an inconsistent equation, arises when there are no possible values for the variable that can satisfy the equality. In other words, no matter what value you substitute for the variable, the equation cannot be true.
Common Forms of Equations with No Solution
- Contradictory Linear Equations: These are linear equations that result in a false statement. For example:
2x+3=2x+52x + 3 = 2x + 52x+3=2x+5
Simplifying this equation leads to:
3=53 = 53=5
Since this statement is false, the original equation has no solution. - Absolute Value Equations: These can also yield no solution. For instance:
∣x∣=−3|x| = -3∣x∣=−3
The absolute value of any number is always non-negative, so there are no values of xxx that can satisfy this equation. - Quadratic Equations: Some quadratic equations may also have no real solutions, particularly when the discriminant is negative. For example:
x2+4x+5=0x^2 + 4x + 5 = 0x2+4x+5=0
The discriminant (b2−4ac)(b^2 – 4ac)(b2−4ac) is:
42−4⋅1⋅5=16−20=−44^2 – 4 \cdot 1 \cdot 5 = 16 – 20 = -442−4⋅1⋅5=16−20=−4
Since the discriminant is negative, this equation has no real solutions; its solutions are complex numbers.
Why Do Equations Have No Solutions?
The primary reason for an equation to have no solution stems from contradictions that arise during the simplification process. Inconsistent equations may result from:
- Logical contradictions: As demonstrated in the contradictory linear equations, where simplification leads to a statement that is always false.
- Domain restrictions: In the case of absolute value equations, where the conditions of the equation contradict the definition of absolute values.
- Negative discriminants: In quadratic equations, indicating that the roots are not real numbers.
Importance of Recognizing No-Solution Equations
Understanding which equations have no solutions is crucial in mathematics and its applications. This knowledge is particularly relevant in fields such as:
- Algebra: Mastery of no-solution equations allows students to understand the limitations of certain equations and the conditions under which they can be solved.
- Engineering and Physics: Engineers and physicists often encounter equations where solutions may not exist, impacting the feasibility of designs and theories.
- Computer Science: Algorithms that rely on solving equations must account for cases where no solution is possible to ensure accurate results.